Квантовая запущенность (2)

justavortex — 16.08.2025

Следующим физиком, работавшим с интерференцией, по факту переоткрывшим ее, давшим ей математическое объяснение и придумавшим несколько еще более любопытных экспериментов, явился Огюстен Жан Френель.

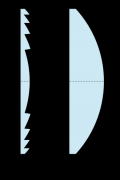
Здесь следует упомянуть о разработанной им линзе, создающей параллельный поток света от точечного источника, 

немедленно нашедшей себе применение в маяках и ставшей прообразом всех современных осветительных приборов — от фар до прожекторов.

Нас же в рамках вопроса, к которому мы постепенно приближаемся, интересуют два других его изобретения, позволивших углубить знания по интерференции. Зеркала и призма Френеля.

Схема с зеркалами Френеля. S — щелевой источник, Z1 и Z2 два зеркала, повернутые друг к другу на минимальное расстояние в несколько угловых минут. Теперь две щели Юнга заменены этими зеркалами, мы получаем два совершенно когерентных излучателя с одинаковым хроматическим характером и картина интерференции, которую в установке Юнга можно было едва различить, здесь видна четко и ясно, по расстояниям между кольцами можно определить весьма точно длину световой волны. Далее, бипризма Френеля.

Та же история: цель, получить два согласованных источника света, при пересечении волн они дадут их взаимное наложение и кольцевую интерференцию.

Совершенствует принцип Гюйгенса, дополняя его рассмотрением когерентных интерферирующих волн. Френель строго доказывает, что последовательное применение волновой картины ведет к прямолинейности световых лучей. Рассматривая по Гюйгенсу все точки сферического светового фронта как источники новых сферических волн, он показывает, что вторичные волны гасятся во всех направлениях, кроме того единственного, который отвечает направлению светового луча. Таким образом, пало главное возражение против волновой оптики.

Закладывает основы кристаллооптики, в нашем с вами вопросе  это также пригодится, заметьте себе. Явление двойного лучепреломления было известно и ранее, но он подвел под это матаппарат. Оно состоит в том, что анизотропные кристаллы могут расщеплять луч на два, при этом выходящие лучи будут иметь разную поляризацию.

Под все описанные выше явления, как и под дифракцию, Френель подвел математическое обоснование, чем снискал и почет и уважение и премию академии наук. Что, впрочем, не мешало ему вести уединенный и весьма скромный образ жизни, тратя личные средства на физические эксперименты. В отличии от Юнга, миллионных наследств ему никто не оставил, а Французская республика содержать не разбежалась, так что он умер 14 июля 1827 года в возрасте 39 лет от туберкулеза, вызванного известной социальной средой и образом жизни. Продолжение следует.

Оставить комментарий

Популярные посты:

titus

Эвакуатор по межгороду и Татарстану: как правильно вызвать службу

millord

Донбасс без воды.

livilla_ass

Судьба предателей. Сначала предали они, потом "кинули" их.

rivka381

Пропавшие без вести. Тыва.

zampolit_ru

Секретный план по Крыму

movie_rippers

«Солдатик» (2018) – этот обзор вам не понравится

mishin05

Жиды - не сапиенсы. В их внешности и повадках просматривается иной подвид хомо

sobakin_spb

Прогулки во сне и наяву ..

13vainamoinen

Картинки из леса

• Ранее
• Архив