Mermin-Peres magic square game

thedeemon — 30.03.2025 Мне тут недавно показали одну занятную штуку на тему "квантовой псевдотелепатии", я стал смотреть как оно устроено, и некоторые детали оказались даже неожиданнее и интереснее, чем основной результат.

Вариант игры с двумя игроками звучит так. Есть ведущий и два игрока: Алиса и Боб, разумеется. Есть доска как для крестиков-ноликов, 3х3. Ведущий выбирает наугад строку и столбец, и просит Алису заполнить строку, а Боба - заполнить столбец. Заполнять они должны какими-то значениями 1 или -1, но так, чтобы произведение значений в строке Алисы получалось 1, а произведение значений в столбце Боба - -1. Игроки изолированы друг от друга, общаются только с ведущим и не знают, какой вопрос другой игрок получил и что он ответил. Если на пересечении строки Алисы и столбца Боба оба поставили одинаковое значение, они выиграли. Если значения не совпали, то они проиграли. В одном раунде игры каждый игрок получает лишь один вопрос (с номером строки/столбца) и дает один ответ (3 бита). Всю доску заполнять не нужно, только одну строку и один столбец. Спрашивается, как бы Алисе и Бобу выигрывать почаще?



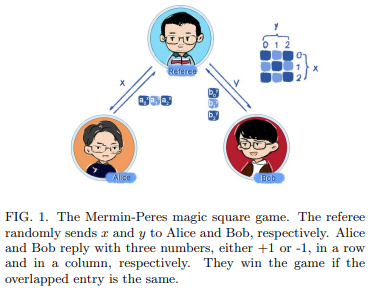
Отвечать рандомно им не слишком выгодно, лучше заранее выбрать стратегию, можно составить шпаргалку с ответами. У Алисы в шпаргалке в каждой строке произведение чисел равно 1, а потому произведение всех 9 чисел тоже 1. Но у Боба в каждом столбце должно быть произведение -1, поэтому произведение всех 9 чисел у Боба должно быть -1. Нет такой таблицы 3х3, которая бы подходила обоим игрокам, но некоторые подходящие Алисе таблицы совпадают с некоторыми подходящими Бобу в 8 ячейках из 9. Используя такие шпаргалки, игроки могут выигрывать в среднем в 8 играх из 9.

А вот если у них будет по паре запутанных нужным образом кубитов, то теоретически они смогут выиграть в 100% случаев! Лет 30 назад Мермин и Перес описали теорию как это сделать, а пару лет назад китайские экспериментаторы смогли это воплотить на практике. Из-за неидеальности оборудования они выиграли не в 100, а в 93.84% случаев, но это все равно намного больше классического предела в 88.89%.

Залог успеха - вот такая табличка операторов, общая для Алисы и Боба:

 I⊗Z   Z⊗I   Z⊗Z
 X⊗I   I⊗X   X⊗X
−X⊗Z  −Z⊗X   Y⊗Y

Тут X,Y,Z - операторы измерения спина вдоль соответствующей оси, дающие 1 или -1, I - единичный оператор, всегда дающий 1. Каждый игрок в каждом раунде берет пару кубитов. Запись вроде X⊗Z означает, что мы у первой частицы меряем спин вдоль X, а у второй меряем спин вдоль Z, результаты (1 или -1) перемножаем, получая одно число. Если Алиса, получив от ведущего номер строки, сделает такие измерения со своей парой частиц/кубитов и получит три числа 1 или -1, а Боб, используя эту же табличку, сделает измерения по своему столбцу, то во-первых их ответы на пересечении строки и столбца совпадут (т.к. меряют одно и то же у нужным образом запутанных частиц), а во-вторых произведения знаков в строке и столбце получатся ровно как правила игры требуют.

Если смотреть на первые две строки или первые два столбца, то все выглядит просто. Например, в первой строке мы у обеих частиц меряем спин вдоль Z, и в первой ячейке результат это спин второй частицы, во второй ячейке - спин первой частицы, в третьей ячейке - их произведение. Если все результаты ячеек перемножить, каждое значение спина поучаствует в произведении ровно дважды, поэтому результат произведения будет всегда 1, как Алисе и требуется.

Но вот если смотреть на третий столбец или третью строку, то там нам нужно измерить спины частиц вдоль всех трех осей. Но как это можно, если каждый ребенок знает, что операторы спина вдоль разных осей не коммутируют, а значит измерить их одновременно нельзя? Нет такого состояния, которое бы имело определенный спин сразу вдоль двух осей. И значит нет такого измерения (measurement), которое дало бы нам значения спина вдоль сразу двух измерений (dimensions). Если спин определен вдоль одной оси, то полностью неопределен вдоль других. Если мерять их по-очереди, то первое же измерение сколлапсирует квантовое состояние, и последующие измерения вдоль других осей во-первых будут совершенно случайными, а во-вторых запутанность кубитов уже будет потеряна.

И вот тут происходит удивительная вещь. Каждый из операторов X,Y,Z представлен своей матрицей Паули размером 2х2.

    |0 1|       |0 -i|        |1  0|
X = |1 0|   Y = |i  0|    Z = |0 -1|

А оператор вроде X⊗Z это их тензорное произведение, он уже представлен матрицей 4х4,

       |0  0 1  0|
       |0  0 0 -1|
X⊗Z = |1  0 0  0|
       |0 -1 0  0|

и вот эти 4х4 матрицы операторов из нашей таблички в каждой строке и каждом столбце меж собой коммутируют! (AB - BA = 0) Получается, что хотя измерить спин одной частицы вдоль двух осей нельзя, но вот измерить (и тут же перемножить) вдоль двух осей для двух частиц сразу уже можно! И даже вдоль всех трех осей можно. В каждой из строк и в каждом из столбцов, стоящие там три оператора меж собой коммутируют, и значит имеют общий базис собственных векторов, и значит можно соорудить такое измерение (measurement), которое даст нам все три ответа.

Но тут следующий вопрос: Алисе нужно получить три числа, а она делает одно измерение. Как? Матрицы операторов там 4х4, и общий базис там из 4 векторов, т.е. такое объединенное квантовое измерение даст 1 из 4 возможных ответов. Но что примечательно, поскольку Алисе нужно выдать три числа 1 или -1, так чтобы их произведение было 1, у нее всего ровно 4 варианта ответа: [1,1,1], [1,-1,-1], [-1,1,-1] и [-1,-1,1]. Ей нужно выбрать одну из этих четырех троек. Так вот, она берет из своей строки таблицы три оператора, находит их общий базис, в этом базисе делает измерение, и каждый из 4 возможных результатов ей дает один из 4 ответов, что она может выдать. Каждый собственный вектор этого объединенного оператора "подписан" одной из троек битов. И каждая такая тройка содержит ответы-результаты отдельных трех операторов из строки таблицы. Аналогично у Боба.

В эксперименте китайцы умудрились два кубита запихать в один фотон: один кубит - поляризация, второй - orbital angular momentum (OAM). Они создают нужным образом запутанную пару фотонов, один летит к Алисе, второй к Бобу. Получив фотон, Алиса или Боб сначала его подают на один расщепитель, где он в зависимости от поляризации летит в одну или другую сторону, а потом пропускают через OAM-to-polarization конвертер и подают на второй расщепитель по поляризации, в итоге фотон прилетает на один из 4 детекторов и дает 1 из 4 ответов. У разных строк и столбцов разные объединенные базисы, выбор строки/столбца ведет к выбору одного из набора конвертеров, которые чуть по-разному преобразуют состояние фотона перед измерением.

Чтобы промоделировать программой квантовый вариант игры, чтобы там запутанность помогала Алисе и Бобу выигрывать каждый раз, нам нужно иметь вектор состояния, содержащий 4 кубита (2 у Алисы, 2 у Боба), это вектор в 2^4 = 16 комплексных измерениях. В начале раунда генерируется вектор, кодирующий нужное запутанное состояние кубитов. Алиса получает номер строки, выбирает по нему базис и коллапсирует наш вектор, проецируя свою часть на этот базис, получая свои 3 бита. Потом Боб получает номер столбца, выбирает по нему базис и коллапсирует оставшийся после Алисы вектор, уже свою часть, так добывает свои 3 бита. Запутанность проявляется в том, что они оба так вот нелокально меняют один общий вектор состояния.

Вот программа, которая это делает для случая, когда Бобу выпадает последний столбец (самый интересный), а Алисе одна из трех строк (тут вызывается расчет для первой, код расчетов для 2 и 3 строк есть, но их вызов закомментирован):

https://gist.github.com/thedeemon/9138abfef64a4018dcc86e3331088912

Для первой строки и последнего столбца, выдавались такие например ответы:
Alice's bits (I⊗Z, Z⊗I, Z⊗Z) => [-1, -1, 1]
Bob's bits (Z⊗Z, X⊗X, Y⊗Y) => [1, 1, -1]
---
Alice's bits (I⊗Z, Z⊗I, Z⊗Z) => [-1, 1, -1]
Bob's bits (Z⊗Z, X⊗X, Y⊗Y) => [-1, -1, -1]
---
Alice's bits (I⊗Z, Z⊗I, Z⊗Z) => [-1, -1, 1]
Bob's bits (Z⊗Z, X⊗X, Y⊗Y) => [1, -1, 1]
---
Alice's bits (I⊗Z, Z⊗I, Z⊗Z) => [-1, -1, 1]
Bob's bits (Z⊗Z, X⊗X, Y⊗Y) => [1, 1, -1]

Видно, что в каждом случае выполнены правила на четность, и последний бит Алисы совпадает с первым битом Боба (т.к. это правый верхний угол поля).

Если добавить вывод состояний и вероятностей. Вот два раунда игры. Исходное состояние кубитов одинаковое в обоих раундах.

state=[0.5, 0.0, 0.0, 0.0, 0.0, 0.5, 0.0, 0.0, 0.0, 0.0, 0.5, 0.0, 0.0, 0.0, 0.0, 0.5]

У Алисы спрашиваем чем заполнить верхний ряд, она проецирует состояние на свой базис, получает одинаковые вероятности, т.е. может любой из 4 ответов выдать какой захочет (или как рандом ляжет).
probs=[0.25, 0.25, 0.25, 0.25]

Допустим, выбрала варинт 01 с битами [-1, 1, -1].

Состояние коллапсирует до
[0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]

Теперь Боба спрашивают про последний столбец. Он это сколлапсированное Алисой состояние проецирует у себя на свой базис и получает такие вероятности ответов:
P_β++ ([1, 1, -1]) = 0.0
P_β+- ([-1, 1, 1]) = 0.4999999999999999
P_β-+ ([1, -1, 1]) = 0.0
P_β-- ([-1, -1, -1]) = 0.4999999999999999

Уже видно, что он может выдать лишь те, что начинаются на -1. Он выдает один из них и все выигрывают.

---
Теперь другой раунд.
Исходное состояние опять
state=[0.5, 0.0, 0.0, 0.0, 0.0, 0.5, 0.0, 0.0, 0.0, 0.0, 0.5, 0.0, 0.0, 0.0, 0.0, 0.5]
те же одинаковые вероятности для Алисы
probs=[0.25, 0.25, 0.25, 0.25]

Но тут ее жребий решает выбрать последний, т.е. [-1, -1, 1].

Состояние коллапсирует до
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0]

Теперь Боба спрашивают про последний столбец. Он это сколлапсированное Алисой состояние проецирует у себя и получает такие вероятности ответов:
P_β++ ([1, 1, -1]) = 0.4999999999999999
P_β+- ([-1, 1, 1]) = 0.0
P_β-+ ([1, -1, 1]) = 0.4999999999999999
P_β-- ([-1, -1, -1]) = 0.0

Теперь он может выбрать лишь те, что начинаются на 1. Он выдает один из них и все выигрывают.

Получается, что нелокальный коллапс общей для них волновой функции кубитов таким вот образом передал Бобу информацию о том, на какой бит заканчивается выбранный Алисой ряд, как бы неявно передается значение, что у них обоих должно совпасть.

Заглянуть напрямую в вектор состояния Боб не может, но результаты измерения его кубитов напрямую зависят от того, что выпало у Алисы, там две непересекающихся пары вариантов, однозначно сообщающие ему ее выбранный бит. Такая вот телепатия. Но т.к. Алиса не контролирует, что ей выпадет и какой бит будет "передан" Бобу, послать какое-то свое сообщение, передать информацию она не может.

Материалы.
Иган про коммутирующие операторы тут: https://www.gregegan.net/SCIENCE/MPMS/MPMS.html
Статья китайских экспериментаторов: https://arxiv.org/pdf/2206.12042

Оставить комментарий

Популярные посты:

• Ранее
• Архив