Читаю тут комменты

world_of_tanks — 29.02.2012 Читаю тут комменты. Про вероятности, распределения, а также попытки их трактовать. от некоторых оборотов глаза кровоточат.
Вопщем, решил я взять на себя нелегкий труд объяснить гуманитарным гуманитариям и людям с "образование 6 классов" как и чего в этом мире происходит.

Под катом будет немного перевода с матана на русский дворовой.
Докторам математических наук смотреть не рекомендуется. Иначе и у вас глаза закровоточат от насилия над высокой наукой.


Итак. Начнём рубать матан.
Небольшая ремарка: Теория вероятностей(и мат статистика тоже) странная наука. По моим ощущениям ее или понимаешь практически сразу или не понимаешь никогда.
1. Вероятность, распределение, рассеивание, вероятность распределения, типа равномерно, па гаусу - это всё неправильные названия. Правильно оно звучит - Закон распределения плотности вероятности.
Вот так вот сложно и заумно. Законов этих - много. Желающие почитать - на википедию.
Нас интересуют 2 закона - закон равномерного и закон нормального(оно же гауссово) распределений. В принципе они покрывают практически все события и процессы, происходящие в реальном мире. И 100% событий в ВоТ.

1. Закон равномерного распределения плотности вероятности.
Лирическое отступление:
Препод уже второй час пытается объяснить ТеорВер тупенькой студентке.
В отчаянии спрашивает: "Ну вот какая вероятность того, что Вы выйдя на улицу встретите динозавра?"
Студентка: "Ну 50%"
Препод: "НО ПОЧЕМУ???!!!"
Студентка: "Ну или встречу, или нет."

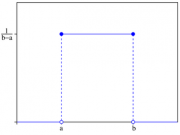
Красивый график с википедии:

Что этот закон означает - он означает, что возникновение любого события из возможных имеет одинаковую вероятность.
На практике - при бросках монетки типа "орел-решка" - именно этот закон.

В ВоТ этому закону подчиняется выбор дамага из диапозона. Крута говорил.

2. Закон нормального распределения плотности вероятности. Еще называют по имени математика Гаусса.
Лирика:
Был такой интересный способ посчитать площадь сложного объекта.
Например, использовался в картографии и метеорологии.
Нужно было посчитать площадь облака - бралась фотка, садился мальчик, который 100(1000, 10000) раз тыкал по ней иголкой, стараясь попасть по центру.
Потом считали коичество точек, попавших в облако и по хитрым формулам вычисляли площадь.

График:

Эт такой интересный закон. он описывает почти все процессы, которые происходят в реальной жизни. Вопщем это такой закон природы - стремиться к равновесию. К среднему значению.
Проще всего прочувствовать этот закон так - выйти на улицу и бросать снежки в стену, метя в середину. Отметины на стене будут распределеню по Гауссу.
За одно - правило 3х сигм.
По-простому, "Три сигмы" - это такая выбока, которая ключает в себя ПРАКТИЧЕСКИ все возможные значения. Кроме самых невероятных. Три сигмы для нормального распределения - 99,7% всех значений.
Сделано так - для облегчения расчетов.
Ну вот с матаном всё. Есть вопросы - в комменты.


Чтоб пост не был сухим и научным - дальше будет секция вопросов Шторму.

1. Почему дамаг рандомится по равномерке, а не по гауссу? Как-то не логично, хотя и добавляет бодрости к БТРу.

2. Вопрос имени Шапочки из фольги.
Время от времени получается такой бой, в котором горят тупо все, а ваншот идет за ваншотом.
Было б смешно, если б небыло так не смешно. И ладно б только я - с удивлением узнал, что и у некоторых других людей такие же наблюдения и сомнения.
В попытке объяснить этот феномен спрошу:
У вас и правда на каждый ВБР запускается рандомайзер?
Или есть прегенеренная таблица в БД со случайными значениями по которой курсор бегает?(я б именно так и сделал, например. да и ваше "три сигмы" косвенно указывают на такой случай).
Если 1 - есть сбои алгоритма при определенных сидах.
Если 2 - где-то в таблице проседания на достаточно большом промежутке.

Оставить комментарий

Популярные посты:

• Ранее
• Архив