Гиппопеда

taurus_ek — 19.06.2023 Сидя на плечах гигантов и свесив ножки, вольно снисходительно поглядывать на остальных гигантов, пошедших неверной дорогой, потому что они еще не знали, какая дорога правильная.


Слепой Орион, ищущий Гелиоса. Пуссен


Грекам долго было невнятно неравномерное движение планет и особенно озадачивали петли, которые планеты описывают на небе.


Попятное движение Марса и Сатурна, APOD

(Такое движение планет в астрономии называется попятным, хотя сейчас из-за влияния англоязычной традиции часто используется термин "ретроградное движение". Кстати, отечественные астрологи его всегда использовали, и по той же причине.)

Из общих соображений греки предполагали, что на небе возможно только правильное круговое и равномерное движение. "Правильность" и единственность такого движения обосновал Аристотель (384 — 322 до н.э.) в своей ранней небольшой, но сложной работе "О небе". Там приводится очень логически выверенное рассуждение со множеством блестящих логических аргументов, беда только в том, что Аристотель принимает изначально ложные физические посылки. Вообще, читая "О небе", видишь каким крутым логиком был автор, но при этом совершенным дилетантом в естественной сфере даже по меркам современников. К сожалению, все они, современники и последователи, были заворожены виртуозными аристотелевскими рассуждениями и априорно отказались от его критики.

Но привлекательность кругового и равномерного движения греками была осознана еще до Аристотеля: обеспокоенный беспорядочным движением светил философ Платон (~428 – 348 до н. э.) предлагает своим ученикам тему дипломной работы задачу: представить движение планет в виде комбинации равномерных круговых движений. Вокруг Земли, естественно.

С задачей справляется Евдокс Книдский (408 год — 355 год до н. э.), сформулировавший теорию гомоцентрических сфер. Для объяснения сложного движения планеты им была предложена система вложенных концентрических сфер, вращающихся друг в друге в разными скоростями и вокруг разнонаправленных осей. Работы Евдокса Книдского не сохранились, но остались описания его теории, а её реконструкцию предложил итальянский астроном Скиапарелли (тот самый, кто открыл марсианские каналы, впоследствии закрытые).


Схема гомоцентрических сфер одной планеты. Из Wikipedia

Первая, внешняя сфера делает один оборот в сутки и ответственна за суточное движение. (Евдокс, в отличие от Аристотеля и его последователей нумерует сферы снаружи к Земле, так что самая внешняя сфера - первая.) Вторая сфера ответственна за среднее движение планеты вдоль эклиптики и делает оборот за сидерический период планеты. Её ось составляет с осью предыдущей сферы угол, равный наклону эклиптики. С первыми двумя компонентами всё понятно.

Третья же и четвертая сферы предназначены для петлеобразного движения. Они несоосны, вращаются в противоположных направлениях, и при этом делают оборот за одно время. Можно показать, что при этих условиях точка (планета), лежащая на экваторе внутренней сферы, будет описывать во внешней системе координат фигуру, напоминающую восьмерку - гиппопеду.



Признаюсь, что у меня не хватает пространственного воображения представить, как формируется эта восьмерка. Понятно, что если сферы соосны, то фигура вырождается в точку. Если же угол отличен от нуля, точка начинает смещаться, и я верю Скиапарелли, что в результате опишет гиппопеду. Пространственного воображения мне хватает на предположение, что в изображенной на схеме ситуации планета находится в центре восьмерки и движется справа вверх налево.

Наконец, ось третьей сферы лежит на экваторе второй, а значит гиппопеда лежит "на боку" на эклиптике, движется "лёжа" по небу, собственно, и формируя петлю ретроградного движения планеты.

Евдокс предложил только идею, но не довел ее до работоспособной модели: в его варианте петли попятного движения должны быть симметричны, но фактически-то это не так. Вероятно, теорию гомоцентрических сфер можно было подрихтовать, но дело до этого не дошло.

Для меня неожиданным бонусом было узнать, что геостационарные спутники, двигающиеся по геосинхронным орбитам, описывают над географической точкой стояния восьмерку. Кинематически геосинхронное движение эквивалентно движению двух внутренних сфер Евдокса, а искажение в форму гиппопеды вносит эксцентриситет орбиты спутника. Вот пример орбиты геостационарного спутника "Молния"


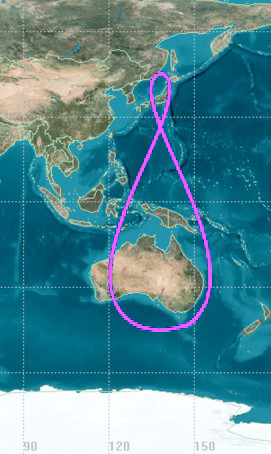
Орбита "Тундра", Википедия

Итак, математически теория гомоцентрических сфер выглядит понятно, но как с физической реальностью для пяти планет (плюс Солнце и Луна: для каждого из светил достаточно трёх сфер, но я не буду на этом задерживаться)? Сферы внутренних планет нельзя прикрепить к "неподвижной основе": эта "неподвижная основа" перекрыта сферами первой наружной планеты, Сатурна. Тория предлагает решение фактически в стиле brute force (и на мой вкус, это никакое не решение). Вот что предлагается. Для каждой сферы необходима "компенсирующая сфера", вращающаяся с той же скоростью, с таким же наклоном, но в противоположную сторону. Компенсирующая сфера 4' погасит вращение сферы 4, следующая сфера 3' погасит вращение сферы 3, затем 2', а вращение сферы 1 гасить не нужно - это общее суточное вращение неба. Таким образом, на-внутри сферы 2' мы можем смело строить комплекс сфер для очередной планеты. Результатом будет 37 вложенных хитроумно синхронизированных сфер.

Решение, конечно, геометрически корректное, но уж больно некрасивое. По этой ли или по иной причине теория гомоцентрических сфер Евдокса Книдского развития не получила.

Оставить комментарий

Популярные посты:

• Архив