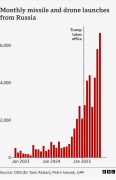
2.3. Стрела времени в статистической механике

evgeniirudnyi — 10.05.2025

Неравенство Клаузиуса является критерием самопроизвольных процессов и поэтому говорят, что оно задает стрелу времени в классической термодинамике. Законы движения Гамильтона симметричны во времени и поэтому поиск аналога неравенства Клаузиуса в статистической механике все еще продолжается. Мы рассмотрим главные аргументы появления асимметрии во времени, в том числе основанные на признании субъективности энтропии и на связи энтропии с информацией.

В этой главе мы рассмотрим начальный этап поиска стрелы времени, который наступил после создания молекулярно-кинетической теории во второй половине 19-ого века. Интересно отметить, что Джеймс Максвелл сразу же понял невозможность этого предприятия в силу симметрии во времени уравнений Гамильтона. В письме Питеру Тэйту в 1873 году Максвелл высмеивал попытки Клаузиуса и Больцмана - демон Максвелла должен был наглядно показать тщетность таких попыток:

'редко можно увидеть, как эти ученые немцы борются за приоритет открытия того, что 2-й закон сводится к принципу Гамильтона ... Принцип Гамильтона находится в месте, не затронутом статистическими соображениями; в то же время немецкие Икары машут своими восковыми крыльями в стране облаков-кукушек (nephelococcygia) среди тех облачных форм, которые невежество и ограниченность человеческой науки наделили непередаваемыми атрибутами невидимой Царицы Небес.'

Тем не менее, работы Людвига Больцмана привели к интересным результатам, включая известное статистическое обоснование второго закона. Вначале мы рассмотрим эволюцию взглядов Больцмана; в ходе обсуждения его попыток доказать неравенство Клаузиуса возникли два парадокса: парадокс механической обратимости Иоганна Лошмидта и парадокс возврата, связанный с теоремой Анри Пуанкаре о возвращении.

Статистическое обоснование энтропии Больцмана было ограничено идеальным одноатомным газом. Гиббс ввел статистическую энтропию в общем случае для произвольной системы. К сожалению, эта статистическая энтропия формально остается постоянной в неравновесном процессе. Таким образом, в общем рассмотрении Гиббса возникло противоречие между формальным математическим выводом и вторым законом термодинамики. Гиббс первым заметил это обстоятельство и предложил возможные решения. В этой главе я остановлюсь на общем обсуждении статистической энтропии Гиббса, а сходство между энтропией Гиббса и информационной энтропией Шеннона будет рассмотрено в последующих главах.

Оставить комментарий

Популярные посты:

credobnik

Топ-5 ошибок при установке полотенцесушителя и как их избежать

skazki_idy

Гляди, чего могу!..

tanjand

Визуальная задачка: что здесь нарисовано

ida_mikhaylova

Не мешаю высказываться

svetan_56

Насколько смертоносна медицина?

nedogurok

Последняя часть фотографий Wildlife Photographer of the Year

a_nalgin

О реках и мостах Почему Россия не «выносит» украинские переправы?

orientalist_v

"Зеркальный образ: сокровище"

pekov

Почему так быстро рвуться г​*****ы?

• Ранее
• Архив